import torch
x = torch.ones(5) # input tensor
y = torch.zeros(3) # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)
テンソル、関数、計算グラフの関係¶
上記のコードは以下の計算グラフ(computational graph)を示しています。
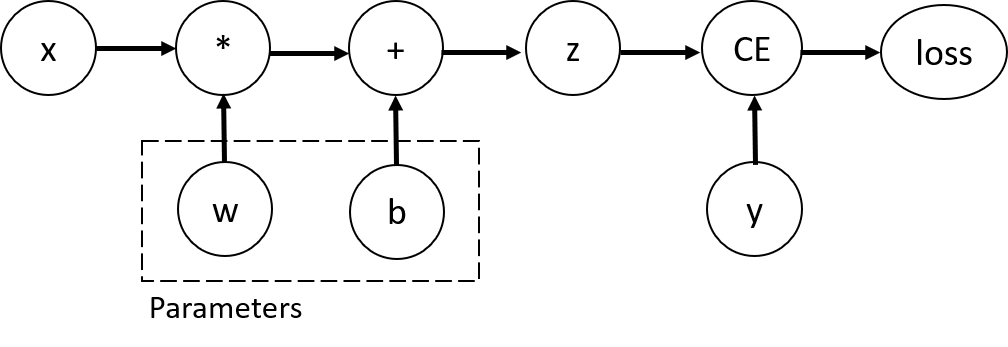
上記のネットワークでは、wとbが最適したいパラメータです。
そのため、これらの変数に対する損失関数の微分値を計算する必要があります。
これらのパラメータで微分を可能にするために、requires_grad属性をこれらのテンソルに追記します。
【注意】
requires_gradはテンソルを定義する際、もしくはその後に、x.requires_grad_(True)を実行するなどして指定できます。
計算グラフを構築する際に、テンソルに適用する関数は実際には Functionクラスのオブジェクトです。
これらオブジェクトでは、順伝搬時に入力をどのように処理するのか定義されています。
加えて、バックプロパゲーション時に勾配をどのように計算するのかも把握しています。
そして勾配は、テンソルの grad_fn プロパティに格納されます。
Functionのさらなる詳細については、こちらを参照ください。
print('Gradient function for z =',z.grad_fn)
print('Gradient function for loss =', loss.grad_fn)
Gradient function for z = <AddBackward0 object at 0x7f7a86429b10> Gradient function for loss = <BinaryCrossEntropyWithLogitsBackward object at 0x7f7a86429b50>
勾配の計算¶
ニューラルネットワークの各パラメータを最適化するために、入力xと出力yが与えられたもとで、損失関数の各変数の偏微分値、
すなわち
$\frac{\partial loss}{\partial w}$ 、$\frac{\partial loss}{\partial b}$
を求める必要があります。
これらの偏微分値を求めるためにloss.backward()を実行し、w.gradとb.gradの値を導出します。
loss.backward()
print(w.grad)
print(b.grad)
tensor([[0.1212, 0.1953, 0.3046],
[0.1212, 0.1953, 0.3046],
[0.1212, 0.1953, 0.3046],
[0.1212, 0.1953, 0.3046],
[0.1212, 0.1953, 0.3046]])
tensor([0.1212, 0.1953, 0.3046])
【注意】
gradは計算グラフのleaf node(かつ、requires_gradがTrueの変数)のみで求めることができます。
全ての変数で勾配が計算できるわけではない点にはご注意ください。
また、勾配の計算は各計算グラフに対して、backwardを実行し、1度だけ計算できます(1度しか計算できないのは、パフォーマンスの観点からの仕様です)。
仮に、同じ計算グラフに対して複数回backwardを実行したい場合には、retain_graph=Trueをbackward時に引数として渡す必要があります。
勾配計算をしない方法¶
デフォルトでは、requires_grad=Trueである全てのテンソルは計算履歴が保持され、勾配計算可能な状態です。
ですが、勾配計算が不要なケースも存在します。
例えば訓練済みモデルで推論するケースなどです。
すなわち、ネットワークの順伝搬関数のみを使用する場合となります。
実装コードで勾配計算を不要にするには、torch.no_grad()のブロックにそれらのコードを記載するようにします。
z = torch.matmul(x, w)+b
print(z.requires_grad)
with torch.no_grad():
z = torch.matmul(x, w)+b
print(z.requires_grad)
True False
同様に、detach() をテンソルに使用することでも実現できます。
z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)
False
勾配の計算、追跡を不能にしたいケースはいく種類かあります。
ネットワークの一部のパラメータを固定したい(frozen parameters)ケース。これはファインチューニング時によくあるケースです。
順伝搬の計算スピードを高速化したいケース。
順伝搬では autograd は2つの処理を同時に行っています。
- 指定された演算を実行し、計算結果のテンソルを求める
- DAGの各操作のgradient function を更新する
逆伝搬では、.backward()がDAGのrootのテンソルに対して実行されると、autogradは、
- 各変数の
.grad_fnを計算する - 各変数の
.grad属性に微分値を代入する - 微分の連鎖律を使用して、各leafのテンソルの微分値を求める
を行います。
【注意】
PyTorchではDAGは動的です(Functionで計算処理される際に逐次構築されていきます)。
そして、.backward()を呼び出すたびに、autogradは再度新しいグラフを作成します。
この特性こそが、モデルの順伝搬時に制御フロー文(if文やfor文)を使える理由であり、必要に応じて反復ごとに形や大きさ、操作を変えることができます。
【日本語訳注】
上記内容は初心者の方には非常に難しい話です。
PyTorchは Define-by-run 形式であり、事前に計算グラフを定義するのではなく、計算を実行する際に、柔軟に計算グラフを作ってくれます。
一方で、Define-and-run形式のディープラーニングフレームワーク(例えば、TensorFlow v1など)は、事前に計算グラフを定義する必要があるため、for文やif文といった制御フローの構文を柔軟に使いづらいです。
このことを上記内容では説明しています。
補注:テンソルに対する勾配とヤコビ行列¶
多くの場合、スカラー値を出力する損失関数に対して、とある変数の勾配を計算します。
ですが、関数の出力がスカラー値ではなく、任意のテンソルであるケースもあります。
このような場合、PyTorchでは実際の勾配ではなく、いわゆるヤコビ行列(Jacobian matrix)を計算することができます。
ベクトル関数 $\vec{y}=f(\vec{x})$,において、 $\vec{x}=\langle x_1,\dots,x_n\rangle$ 、そして $\vec{y}=\langle y_1,\dots,y_m\rangle$の場合、
その勾配、 $\vec{y}$ with respect to $\vec{x}$ はヤコビ行列 で与えられます。
\begin{split}\begin{align}J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\end{align}\end{split}
ヤコビ行列そのものを計算する代わりにPyTorchでは、Jacobian Product、 $v^T\cdot J$ を、入力ベクトル$v=(v_1 \dots v_m)$ に対して計算します。
これは、$v$を引数として backwardメソッドを呼び出すことで計算されます。
なお$v$ のサイズは積を計算したい、元のテンソルの大きさと同じである必要があります。
inp = torch.eye(5, requires_grad=True)
out = (inp+1).pow(2)
out.backward(torch.ones_like(inp), retain_graph=True)
print("First call\n", inp.grad)
out.backward(torch.ones_like(inp), retain_graph=True)
print("\nSecond call\n", inp.grad)
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print("\nCall after zeroing gradients\n", inp.grad)
First call
tensor([[4., 2., 2., 2., 2.],
[2., 4., 2., 2., 2.],
[2., 2., 4., 2., 2.],
[2., 2., 2., 4., 2.],
[2., 2., 2., 2., 4.]])
Second call
tensor([[8., 4., 4., 4., 4.],
[4., 8., 4., 4., 4.],
[4., 4., 8., 4., 4.],
[4., 4., 4., 8., 4.],
[4., 4., 4., 4., 8.]])
Call after zeroing gradients
tensor([[4., 2., 2., 2., 2.],
[2., 4., 2., 2., 2.],
[2., 2., 4., 2., 2.],
[2., 2., 2., 4., 2.],
[2., 2., 2., 2., 4.]])
上記において、同じ変数inpに対して、backwardを2回目実行した際には、勾配が異なる値になった点に注意してください。
これはPyTorchではbackwardを実行すると、勾配を蓄積(accumulate)する仕様だからです。
すなわち、計算グラフの全leafのgradには、勾配が足し算されます。
そのため適切に勾配を計算するには、gradを事前に0にリセットする必要があります。
なお実際にPyTorchでディープラーニングモデルの訓練を行う際には、オプティマイザー(optimizer)が、勾配をリセットする役割を担ってくれます。
【注意】
本チュートリアルの最初の方で、backward()関数を引数のパラメータなしに実行していました。
これは実質的には、backward(torch.tensor(1.0))を実行しているのと同じとなります。
backward()はスカラー値の関数(例えば訓練時の損失関数)に対して、各パラメータの勾配を計算する際に便利です。
以上。